今回はばねの種類!なんですが、コイルバネの解説だけです。
さあ、コイルバネは最も基本となるばね。そして実用例が最も多いばねでもあります。一応種類としては圧縮、引張、ねじりの3つが主にありますが、その中でも圧倒的に採用例の多い圧縮コイルバネについて今回は扱っていきます。後半はシリーズ初となる理論もありますので頑張ってついてきてくださいね。
概要
まずは概要から。コイルバネは素線(細い棒状の材)をコイル状に加工したものです。「ばね」と言えばコイルバネを想像される方が大半だとは思います。
メリットは
・ストローク(変位量)が大きい
・中央の空間もダンパ等で利用可能
・大量生産技術が確立されており安価
一方デメリットは
・減衰なし(むしろ発条としては当たり前)
・省スペースには不向き
こんなもんでしょうか。とはいえ、基本のばねだけあって、コイルばねが使えないor他のばねの長所が生かせる特殊な状況がない限りは最優先で使用されます。そのためメリットデメリットについてそこまで深く考えたことはないですし、あまり語られることもないように思います。
そのため使用例は圧縮コイルバネだけでも多岐にわたります。そのため今後のコイルばね以外のばねの使用例でコイルバネがどういった場面では使われないのかを読んでいただければおkです。
ばね定数とは(コイルバネ編)
ということで理論ですね。ばね定数とは何ぞや?という話。コイルバネを下図のように定義しましょう。
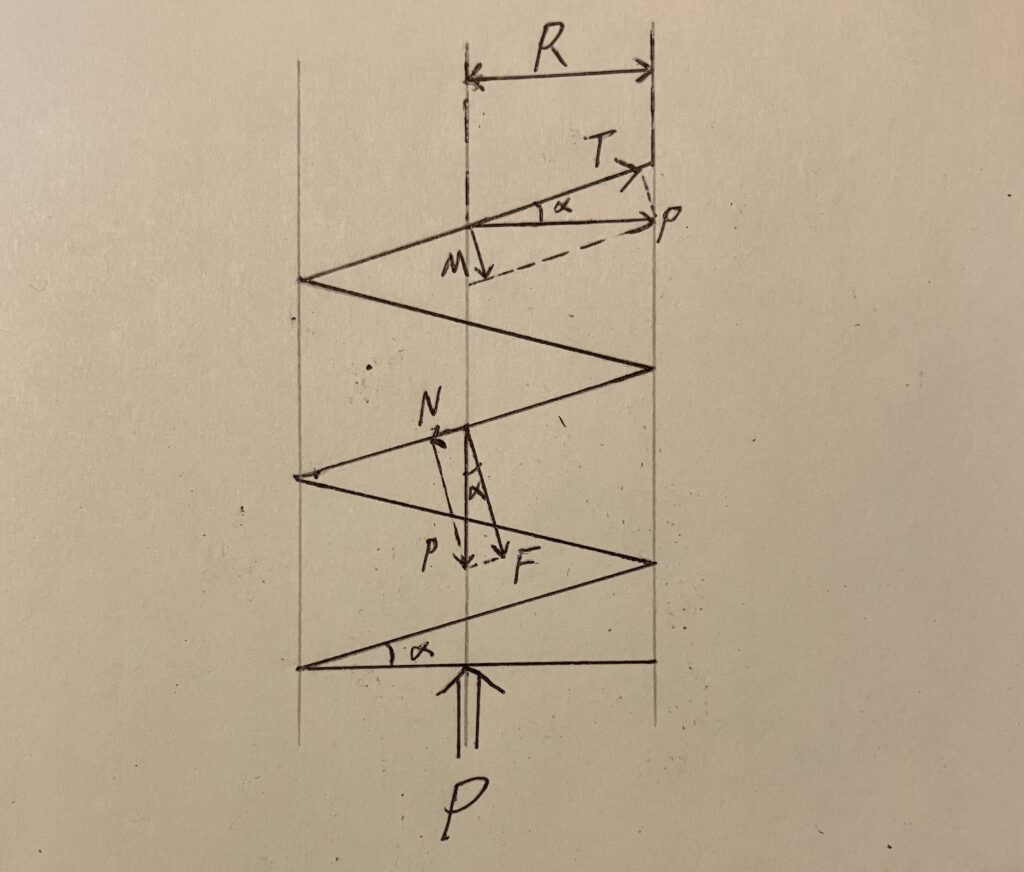
すると、コイルバネの素線には以下のような力が働いていると考えることができます。
引張力 \(N=P\sin\alpha\) (1)
せん断力 \(N=P\cos\alpha\) (2)
曲げモーメント \(M=PR\sin\alpha\) (3)
ねじりモーメント \(T=PR\cos\alpha\) (4)
ここで、コイルバネの伸びについて考えます。コイルバネにおいて伸びはねじりモーメントにより発生するものであると考えることができます…が、これについて一応説明しておきましょう。まず、材料の弾性変形において考えるのは主に「引張(圧縮)」と「曲げ」そして「ねじれ」の3種類です。せん断は今回パス。今回はコイルバネについて考えていますが、全体を見ているとわかりにくいので一部分を切り取って大きく変形させてみます。この段階で引張力は加わっていないのが想像できると思います。ではここからさらに短い区間について見ていきます。
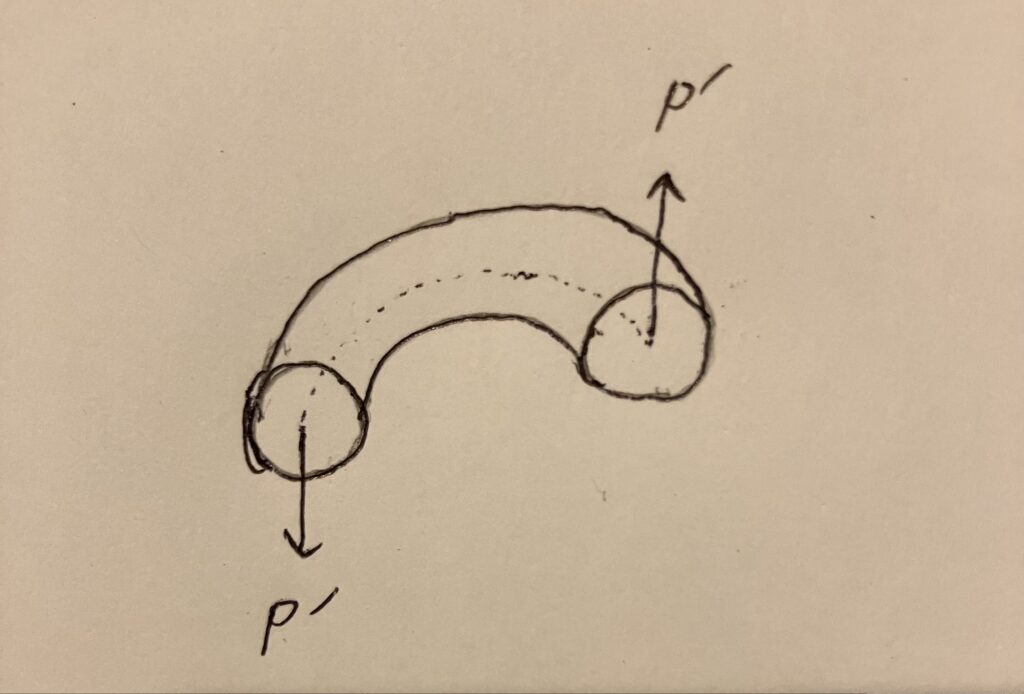
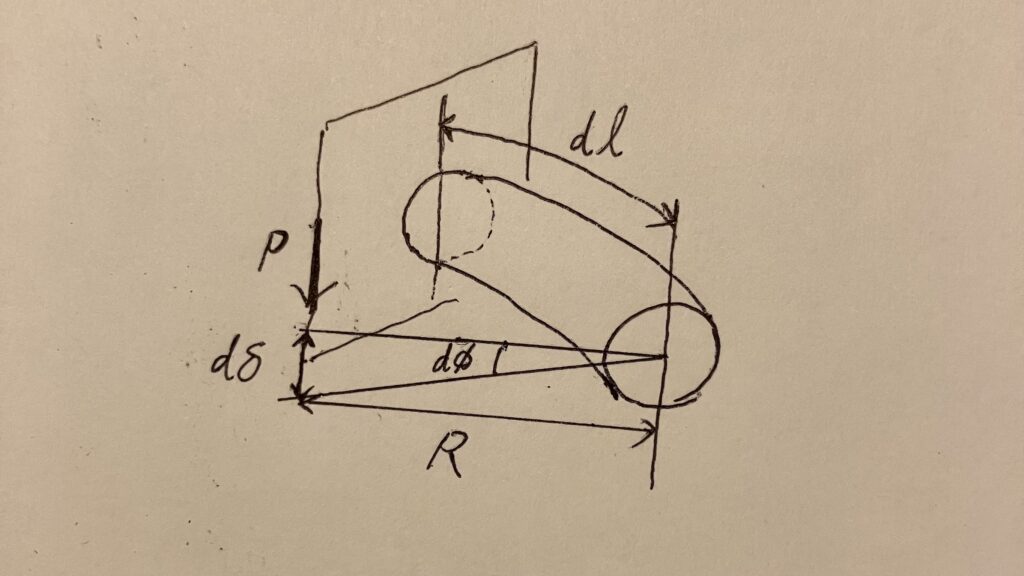
ここで曲げが働かないことが分かると思います。 ということで、コイルバネの伸びに関してはねじれのことのみを考えればよいわけです。また、式(1)、(3)より引張力Nと曲げモーメントMはα(アルファ)が微小ならば0に近似できることからも明らかです。ということで素線の微小区間dlにおけるねじれモーメントTによるねじれ角dφについて考えます。これは、式(5)であらわされます。この式自体はあらゆる等方性材料のねじれについて適用できます。
\(d\phi=\frac{Tdl}{GI_p}\) (5)
ここでGは横弾性係数、Ipは断面二次極モーメントです。これは今のところあまり大事ではないので、次のことを覚えていただければ大丈夫です。それは「横弾性係数と断面二次極モーメントの積はねじれ剛性」ということです。つまり材料のねじれにくさを表します。ということは式を言語化すると以下のようになります。
\((ねじれ角)=\frac{(力の大きさ)\times(素線の長さ)}{(ねじれ剛性)}\)
力の大きさや素線の長さが長くなればねじれは大きくなり、ねじれ剛性が大きくなるとねじれは小さくなると。極々当たり前のことを言っているに過ぎないだけです。
さて、ねじれ角が分かったのならばばねの伸びもわかるはずです。ということで、このねじれ角によるコイル中心線上の垂直変位は式(6)であらわされます。
\(d\delta=Rd\phi=\frac{RT}{GI_p}dl\) (6)
これはあくまで微小区間の話なので、ばね全体に拡張してあげます。
\(\delta=\int_0^l\frac{RT}{GI_p}dl=\frac{RT}{GI_p}l\) (7)
これでばねの伸びについて示すことができました。このままでも問題はないのですが、実際には断面二次極モーメントは計算値ですし、ばねの長さについても正確に計測するのは面倒くさいです。そこで正確な計測が簡単な値をそのまま代入できるようにしていきます。具体的にはばねの長さをコイルの巻き数Nで(式(8))、断面二次極モーメントを素線の直径dで(式(9))表していきます。
\(l\simeq2\pi RN\) (8)
\(I_p=\frac{\pi d^4}{32}\) (9)
これらに加え、式(4)、(8)、(9)を式(7)に代入すると、
\(\delta=\frac{RT}{GI_p}l=\frac{64NPR^3}{Gd^4}\cos\alpha\approx\frac{64NPR^3}{Gd^4}\) (10)
なお、式(8)及び式(10)はαが十分に小さいと仮定しています。因みに三角関数において「十分に小さい」とは大体14 degree以下と思っていただければ。これは誤差1%以内に収まる角度。日常的に見かけるコイルバネではこれを満たすことがほとんどだと思います。さあ、ここでフックの法則より、ばね定数kを導くことができます。
\(k=\frac{P}{\delta}=\frac{Gd^4}{64NR^3}\) (11)
ということで、ばねの性質で最も重要なばね定数kは素線の物性値(横弾性係数G)、素線の直径d、コイルの巻き数N、コイルの半径Rで求めることができるということが分かりました。さらに、ばね定数において(指数関数的な増減を示すため)素線の直径とコイル半径は重要なパラメータであるということが分かると思います。
また、今回は途中で断面二次極モーメントを展開して代入しましたが、そのままの状態だと面白いことが分かります。それは、素線の断面形状でもばね定数は変更できるという点です。通常は円形ですが、これを太さが等しい正方形断面に変更するだけでばね定数は増加します。(断面二次極モーメントが増加するため)
ということで今回はここまで。ちょっと難しかったかもしれませんが工学部ってこういうことをやっているわけですよ。次回以降はいちいちこういうことはやりませんが同様の計算によりばね定数を求めることができるので暇な方はやってみてもいいかもしれませんね。なお、Wikipediaではばね定数の式が少々異なりますが、それはコイル半径ではなくコイル直径を採用しているからです。計測しやすさでいうと直径の方がいいんですけど計算そのものは半径の方が簡単なのでこうしてます。まあ半径⇆直径変換は楽勝でしょう。それではまた次回。



コメント